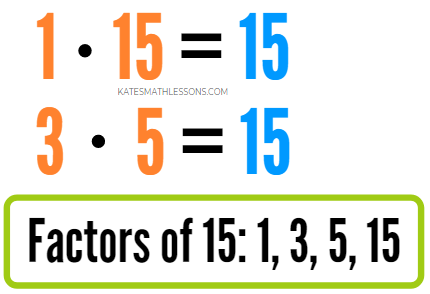
What is the factor pair of 15?
In Stock
$34.99
$29.99
Shipping and Returns Policy
- Deliver to United States » Shipping Policy «
- - Shipping Cost: $5.99
- - Handling time: 2-3 business days
- - Transit time: 7-10 business days
- Eligible for » Returns & Refund Policy « within 30 days from the date of delivery
About ... Regulates food intake, energy expenditure and body weight in response to metabolic and toxin-induced stresses (PubMed:28953886, PubMed:28846097, PubMed: ... An age-support serum containing a 15% solution of growth factors to help minimize and repair visible skin damage to regenerate the look of aging skin. Oct 2, 2023 ... Safety Factor above 15 isn't shown as it isn't typically relevant or calculated. TheCADWhisperer_1-1696336197656.png. @agepfert067. Can you File ... Our results indicate that GDF-15 is an effective biomarker in patients with metastatic colorectal cancer with better sensitivity than CA19-9 and same ... Apr 24, 2007 ... Herein, we identify the Kruppel-like factor 15 (KLF15) as an inhibitor of cardiac hypertrophy. Myocardial expression of KLF15 is reduced in ... A ready-to-use microwell, strip plate ELISA (enzyme-linked immunosorbent assay) Kit for analyzing the presence of the growth differentiation factor 15 (GDF15) Mar 22, 2018 ... GDF15 secreted by leukemic cells was involved in the morphological remodeling of marrow adipocytes, which can in turn promote leukemic cell ... Jun 14, 2019 ... FGF15/19 is now recognized as a transversal metabolic coordinator at the crossroads of the gut, liver, brain and white adipose tissue. The award decision is based on evaluation factors and significant subfactors that are tailored to the acquisition. ... factor ( 15 U.S.C. 637(d)(4)(G)(i) ). (5) ... The aim of this study was to evaluate whether growth differentiation factor-15 (GDF-15) plasma concentration at the time of percutaneous coronary ...
Find similar items here:
what are the factors of 15
- 5 15 25 75 15
- Prime
- How are the factors of a positive number related to the factors of its negative counterpart? If 'a' is a factor of 15, is '-a' also a factor of 15? List all the integer factors of 15. Consider the number line. Can you visualize the factors of 15 on it? How can you use a Venn diagram to represent the common factors of 15 and another number? Create a Venn diagram for the factors of 15 and the factors of 20. Identify the intersection of the two circles in the Venn diagram. What does it represent? What are the applications of understanding factors in real life? Think about scenarios where you might need to divide 15 into equal parts. How is understanding factors helpful in sharing 15 items equally among a group? Consider dividing tasks or resources into equal portions. How do factors play a role? Are factors related to ratios and proportions? If a ratio is simplified using common factors, what does that mean? How can you determine if one number is a factor of another by using division? Perform the division 15 ÷ 1, 15 ÷ 3, 15 ÷ 5, and 15 ÷ 15. What do you observe? What does a remainder of zero indicate in a division problem related to factors? If you divide 15 by 2, do you get a remainder of zero? What does this tell you? Explain why 2 is not a factor of 15 using division. Can you use a calculator to check if a number is a factor of 15? How would you use a calculator to determine if 7 is a factor of 15? What operation would you perform, and what result would you expect if it were a factor? Is the concept of factors only applicable to whole numbers? What are factors in the context of polynomials? (This might be beyond the scope of basic factors of 15) However, consider if the question could be interpreted more broadly in higher mathematics. Focus back on integer factors of 15. Can you list the factors of 15 in ascending order? Can you list the factors of 15 in descending order? What patterns do you notice in the list of factors? How can you pair the factors of 15 such that their product is 15? Multiply each factor of 15 by another factor to see if the product is 15. What does it mean for a number to be a perfect divisor of 15? Are all factors of 15 perfect divisors of 15? Can you think of a number that is a divisor of 15 but not a factor (in the strict definition)? The terms "divisor" and "factor" are often used interchangeably. Understand the nuance, if any. In elementary number theory, are factors typically considered positive? If the context specifies integer factors, then negative numbers are included. Assume the context is positive integer factors unless otherwise specified. How many pairs of positive factors does 15 have? What are these pairs? How is the number of factors related to the prime factorization of a number? The prime factorization of 15 is 3 x 5. How does this relate to its 4 factors? Consider another number, like 12 (2^2 x 3), and its factors. Can you see a pattern? The exponents in the prime factorization play a role in the number of factors. For 15 (3^1 x 5^1), the number of factors is (1+1) x (1+1) = 4. Verify this by listing the factors of 15. Can you predict the number of factors of another number, like 30, using its prime factorization? The prime factorization of 30 is 2 x 3 x 5 (2^1 x 3^1 x 5^1). The number of factors of 30 should be (1+1) x (1+1) x (1+1) = 8. List the factors of 30 to confirm this. How can you use the concept of factors to solve word problems? Example If you have 15 apples and want to divide them equally among some friends, the number of friends must be a factor of 15. What are the possible numbers of friends? Provide other word problem scenarios where factors are useful. Consider problems involving arrangements, groupings, or equal distribution. If you have 15 tiles, what are the possible dimensions of a rectangular arrangement? The dimensions represent the factors of 15. Think about the factors in terms of rows and columns. What if you are asked to find two numbers that multiply to give 15? These are the factor pairs. List all the pairs of numbers whose product is 15. Consider both positive and negative integer pairs. How does understanding factors help in simplifying algebraic expressions? For example, factoring out a common factor from terms. While not directly about the factors of 15, the underlying concept is related. Focus on the arithmetic factors of 15. Can you create a quiz with questions about the factors of 15? Question 1 What are the positive factors of 15? Question 2 How many factors does 15 have? Question 3 Is 7 a factor of 15? Continue creating quiz questions related to the factors of 15. Include questions about prime factors, factor pairs, and divisibility. What is a factor rainbow for the number 15? Draw a factor rainbow connecting the factor pairs of 15. Start with the smallest and largest factors, then connect the next smallest and next largest, and so on. How does the factor rainbow visually represent the factors and their pairs? Can you explain the relationship between factors and the area of a rectangle with a fixed area of 15? If the area of a rectangle is 15 square units and the side lengths are whole numbers, the possible side lengths are the factors of 15. The factor pairs represent the possible dimensions (length and width) of the rectangle. How can you use prime factorization to determine if one number is a factor of another? Example Is 3 a factor of 15? Prime factorization of 3 is 3. Prime factorization of 15 is 3 x 5. Since all prime factors of 3 are present in the prime factorization of 15, 3 is a factor of 15. Example Is 7 a factor of 15? Prime factorization of 7 is 7. Prime factorization of 15 is 3 x 5. Since 7 is not a prime factor of 15, 7 is not a factor of 15. Apply this method to check if other numbers are factors of 15. Is 1 a factor of 15? (Prime factorization of 1 is an empty product). By definition, 1 is a factor of every integer. Is 15 a factor of 15? Prime factorization of 15 is 3 x 5, which is present in itself. What are the divisors of 15 in the set of natural numbers? What are the divisors of 15 in the set of whole numbers? What are the divisors of 15 in the set of integers? How does the set of numbers (natural, whole, integer) affect the list of divisors? Natural numbers 1, 2, 3, ... Whole numbers 0, 1, 2, 3, ... (Note 0 does not divide any non-zero number) Integers ..., -3, -2, -1, 0, 1, 2, 3, ... Focus on non-zero divisors for the context of factors. The positive factors are usually the primary focus unless specified otherwise. How can you use a sieve method (like the sieve of Eratosthenes) to find factors? While the sieve of Eratosthenes is for finding prime numbers, the underlying principle of checking divisibility can be adapted. Consider numbers up to 15 and check if they divide 15 evenly. This is essentially trial division. What are the properties of the number 15 related to its factors? 15 is an odd number. All its factors (1, 3, 5, 15) are also odd. Is this always true for factors of odd numbers? 15 is a composite number because it has more than two factors. 15 is not a perfect square. What is the sum of the reciprocals of the factors of 15? The reciprocals are 1/1, 1/3, 1/5, 1/15. Find their sum. How is the sum of the reciprocals of the factors related to the sum of the factors? (Sum of reciprocals) = (Sum of factors) / (The number itself) Verify this for 15. Sum of factors = 1 + 3 + 5 + 15 = 24. Sum of reciprocals = 1 + 1/3 + 1/5 + 1/15 = 15/15 + 5/15 + 3/15 + 1/15 = 24/15. What is the harmonic mean of the factors of 15? The harmonic mean is the number of terms divided by the sum of the reciprocals. For 15, harmonic mean = 4 / (24/15) = 4 * (15/24) = 60/24 = 5/2 = 2.5. Are there any interesting mathematical facts related to the number 15 and its factors? 15 is a triangular number (1 + 2 + 3 + 4 + 5). Does this relate to its factors? (Not directly) 15 is the product of two consecutive numbers times a third (1 x 3 x 5 is not 15). 15 is the sum of the first four triangular numbers (1 + 3 + 6 + 10 = 20, not 15). Consider the totient function φ(15), which counts the number of positive integers up to 15 that are relatively prime to 15. φ(15) = 15 * (1 - 1/3) * (1 - 1/5) = 15 * (2/3) * (4/5) = 8. This involves the prime factors. What is the square-free part of 15? (The product of the distinct prime factors) For 15, it is 3 x 5 = 15. What is the radical of 15? (Same as the square-free part for square-free numbers) For 15, it is 15. Can you relate the factors of 15 to modular arithmetic? Consider remainders when numbers are divided by the factors of 15. If a number is divisible by 3 and 5, it is divisible by 15. This relates to the prime factors. What are the divisors of 15 in the Gaussian integers? (Numbers of the form a + bi, where a and b are integers, and i is the imaginary unit) The factors in Gaussian integers would include (1, -1, i, -i) multiplied by the usual factors and also factors involving combinations due to the properties of Gaussian integers. This is a more advanced topic. Stick to standard integer factors for the primary focus. Review the definition of a factor once more to ensure clarity. A factor of a number is an integer that divides the number exactly (without leaving a remainder). Apply this definition to 15 to confirm the factors. Consider potential misconceptions about factors. Are multiples sometimes confused with factors? A multiple of 15 is a number obtained by multiplying 15 by an integer (e.g., 15, 30, 45). A factor of 15 divides 15 evenly. How can you differentiate between factors and multiples clearly? Factors are smaller than or equal to the original number (for positive factors). Multiples are greater than or equal to the original number. Can you use a diagram to illustrate the relationship between factors and multiples of 15? A number line showing factors dividing 15 and multiples being divisible by 15. Consider the factor pairs graphically. If you plot points (x, y) such that x * y = 15, where x and y are positive integers, the points will correspond to the factor pairs. The points would be (1, 15), (3, 5), (5, 3), (15, 1). If you only consider unique pairs, it would be related to the number of factors. How does the concept of factors extend to areas other than basic arithmetic? In computer science, factors can be relevant in algorithms involving division or optimization. In cryptography, prime factorization (related to factors) is crucial. Consider the factors of numbers close to 15, like 14 and 16. Factors of 14 1, 2, 7, 14. Factors of 16 1, 2, 4, 8, 16. Compare the number and types of factors. How does being prime or composite affect the number of factors? Prime numbers (like 7) have exactly two factors 1 and themselves. Composite numbers (like 15) have more than two factors. What if you were asked for the common factors of 15 and a prime number other than 3 or 5 (e.g., 7)? Factors of 15 1, 3, 5, 15. Factors of 7 1, 7. The only common factor is 1, so they are relatively prime. What if you were asked for the common factors of 15 and one of its prime factors (e.g., 3)? Factors of 15 1, 3, 5, 15. Factors of 3 1, 3. The common factors are 1 and 3. Consider the greatest common divisor (GCD) and least common multiple (LCM) involving 15. GCD(15, x) is the largest factor that 15 and x share. LCM(15, x) is the smallest multiple that 15 and x share. Example GCD(15, 20) = 5 (common factors are 1, 5). LCM(15, 20) = 60 (multiples of 15 15, 30, 45, 60...; multiples of 20 20, 40, 60...). The relationship between GCD, LCM, and the product of two numbers GCD(a, b) * LCM(a, b) = a * b. Verify this for 15 and 20 5 * 60 = 300, and 15 * 20 = 300. How can you use the factors of 15 to understand divisibility rules? A number is divisible by 15 if and only if it is divisible by both 3 and 5 (the prime factors of 15). Check if a number is divisible by 3 (sum of digits is divisible by 3) and by 5 (ends in 0 or 5). Example Is 45 divisible by 15? Divisible by 3 (4+5=9), divisible by 5 (ends in 5). Yes. Example Is 32 divisible by 15? Not divisible by 3 (3+2=5), not divisible by 5 (ends in 2). No. Can you create a visual aid or chart summarizing the factors of 15 and their properties? A table with columns for factor, type (prime/composite), factor pair, etc. Factor
- title2
- Is the prime factorization of a number unique? How can you use division to find the factors of 15?
- What are the factors of 15?
- -----------
- What is the product of the factors of 15? How do you calculate the product of the factors of a number? Are there any patterns in the factors of numbers?
- Have we found all the factor pairs of 15? Are there any other numbers that divide evenly into 15?
- How does the fundamental theorem of arithmetic relate to factors? Can you express 15 as a product of its prime factors?
-
Next Day Delivery by USPS
Find out more
Order by 9pm (excludes Public holidays)
$11.99
-
Express Delivery - 48 Hours
Find out more
Order by 9pm (excludes Public holidays)
$9.99
-
Standard Delivery $6.99 Find out more
Delivered within 3 - 7 days (excludes Public holidays).
-
Store Delivery $6.99 Find out more
Delivered to your chosen store within 3-7 days
Spend over $400 (excluding delivery charge) to get a $20 voucher to spend in-store -
International Delivery Find out more
International Delivery is available for this product. The cost and delivery time depend on the country.
You can now return your online order in a few easy steps. Select your preferred tracked returns service. We have print at home, paperless and collection options available.
You have 28 days to return your order from the date it’s delivered. Exclusions apply.
View our full Returns and Exchanges information.
Our extended Christmas returns policy runs from 28th October until 5th January 2025, all items purchased online during this time can be returned for a full refund.
No reviews yet. Only logged in customers who have purchased this product may leave a review.